动手学深度强化学习

作者：子鱼

你现在正在阅读的是本教程的0.1alpha版本，可能过于简明，未来的更新将会逐步添加内容并提升友好度，如果可能的话还会加入最新的研究进展。以CC BY-NC-SA 4.0协议共享。

本教程基于Pytorch实现，所有代码在Python 3.8.5 + Pytorch 1.8.1+cu111环境下运行通过。我们假设读者熟悉深度学习，Pytorch，并对于基本的强化学习思想有“名词党”式的了解。没有看过Barto和Sutton的经典《强化学习》砖头书的同学也不要害怕，本教程不会太注重数学细节，而注重算法的想法和程序实现。

欢迎对本译文提出宝贵意见，可邮件至subfishzhou@gmail.com

介绍

强化学习简介

总问题：在环境中为实现优化目标做出序列决策。

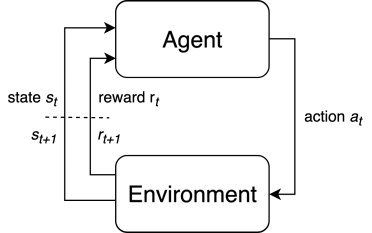强化学习整体框架 图1：强化学习MDP问题整体框架

要素：状态$s_t\in \mathcal{S}$，动作$a_t\in\mathcal{A}$，奖励$r_t\in\mathcal{R}$。

条件：马尔可夫性：后一个状态仅依赖于前一个状态，即$s_{t+1}\sim P(s_{t+1}|s_t,a_t)$。满足此性质的决策问题称为马尔可夫决策过程（Markov decision process，MDP），绝大多数的决策问题都满足此条件，本教程也只考虑MDP问题的求解。

要学习的函数

一个智能体为了实现最大化的总回报，要做出一系列的决策。这些决策可以用一些函数来表示和生成：

  • 策略函数$\pi:\mathcal{S}\rightarrow\mathcal{A}$，表示智能体在某状态下要执行何种动作的函数。
  • 价值函数$V^{\pi}(s)$或$Q^{\pi}(s,a)$，作为期望收益$\mathbb{E}_\tau[R(\tau) ]$的估计。
  • 环境模型$P(s' | s,a)$，表示在某种状态下做出某种动作时向下一个状态转移的概率。

策略函数是最直接的生成策略的依据。例如AlphaGo的走子网络：根据当前棋盘局面（状态）判断下一手的位置。价值函数表示的是每一种可能的状态或行动能带来多大收益，用于间接生成策略，生成的方式可以是贪心的——每一次行动都按照当前最大的收益来实施，也可以是$\epsilon$-贪心的——由于价值函数的估计并不一定反映真实情况，我们只以$\epsilon$的概率实施贪心策略，同时以$1-\epsilon$的概率探索新策略来丰富价值函数的估计。环境模型表示智能体对环境的认识，并由此能够预测自己的行动能够带来什么影响。

深度强化学习算法

深度强化学习对经典强化学习的提升在于，使用“最强函数拟合器”深度神经网络来表示要学习的函数。根据不同算法使用深度神经网络来表示的函数不同，Deep-RL算法可以分成如下的类别：

基于策略的方法：

  • REINFORCE

基于价值的方法：

  • SARSA
  • DQN：Deep Q-Network
  • Double DQN
  • DQN + Prioritized Experience Replay 先验经验回放
  • QT-OPT

基于模型的方法：

  • iLQR：Iterative Linear Quadratic Regulator
  • MPC：Model Predictive Control
  • MCTS：Monte Carlo Tree Search

价值和策略结合的方法：

  • Actor-Critic：
    • A2C：Advantage Actor-Critic
    • GAE：Actor-Critic with Generalized Advantage Estimation
    • A3C：Asynchronous Advantage Actor-Critic
  • TRPO：Trust Region Policy Optimization
  • PPO：Proximal Policy Optimization
  • SAC：Soft Actor-Critic

模型和价值或和策略结合的方法：

  • Dyna-Q / Dyna-AC
  • AlphaZero
  • I2A：Imagination Augmented Agents
  • VPN：Value Prediction Networks

REINFORCE算法

REINFORCE算法是由Ronald J. Williams在1992年的论文《联结主义强化学习的简单统计梯度跟踪算法》（Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning）中提出的基于策略的算法。

REINFORCE算法的想法很自然：在学习过程中，产生高收益的行动应该多做些，导致坏结果的行动应该少做点。我们希望成功的学习结果会让策略函数收敛到能在环境中表现最好的情况。策略函数中动作概率的更新是由策略梯度实现的，因此REINFORCE被称为策略梯度算法。

通过这个想法，我们即将设计的算法会有三个主要组件：

  1. 一个策略函数，里面有一些参数，这些参数在学习过程中将要被更新；
  2. 一个要最大化的目标，能给策略提供即时评价；
  3. 一个参数更新方法。
from torch.distributions import Categorical
import gym
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
gamma = 0.99

class Pi(nn.Module):
    def __init__(self, in_dim, out_dim):
        super(Pi, self).__init__()
        layers = [
            nn.Linear(in_dim, 64),
            nn.ReLU(),
            nn.Linear(64, out_dim),
        ]
        self.model = nn.Sequential(*layers)
        self.onpolicy_reset()
        self.train() # set training mode

    def onpolicy_reset(self):
        self.log_probs = []
        self.rewards = []

    def forward(self, x):
        pdparam = self.model(x)
        return pdparam

    def act(self, state):
        x = torch.from_numpy(state.astype(np.float32)) # to tensor
        pdparam = self.forward(x) # forward pass
        pd = Categorical(logits=pdparam) # probability distribution
        action = pd.sample() # pi(a|s) in action via pd
        log_prob = pd.log_prob(action) # log_prob of pi(a|s)
        self.log_probs.append(log_prob) # store for training
        return action.item()

    def train(pi, optimizer):
        # Inner gradient-ascent loop of REINFORCE algorithm
        T = len(pi.rewards)
        rets = np.empty(T, dtype=np.float32) # the returns
        future_ret = 0.0
        # compute the returns efficiently
        for t in reversed(range(T)):
            future_ret = pi.rewards[t] + gamma * future_ret
            rets[t] = future_ret
        rets = torch.tensor(rets)
        log_probs = torch.stack(pi.log_probs)
        loss = - log_probs * rets # gradient term; Negative for maximizing
        loss = torch.sum(loss)
        optimizer.zero_grad()
        loss.backward() # backpropagate, compute gradients
        optimizer.step() # gradient-ascent, update the weights
        return loss

    def main():
        env = gym.make('CartPole-v0')
        in_dim = env.observation_space.shape[0] # 4
        out_dim = env.action_space.n # 2
        pi = Pi(in_dim, out_dim) # policy pi_theta for REINFORCE
        optimizer = optim.Adam(pi.parameters(), lr=0.01)
        for epi in range(300):
            state = env.reset()
            for t in range(200): # cartpole max timestep is 200
                action = pi.act(state)
                state, reward, done, _ = env.step(action)
                pi.rewards.append(reward)
                env.render()
                if done:
                    break
            loss = train(pi, optimizer) # train per episode
            total_reward = sum(pi.rewards)
            solved = total_reward > 195.0
            pi.onpolicy_reset() # onpolicy: clear memory after training
            print(f'Episode {epi}, loss: {loss}, \
            total_reward: {total_reward}, solved: {solved}')

if __name__ == '__main__':
    main()